Recommendation Info About What Is A Closed Path

Defining the Closed Path: A Formal Perspective
What Exactly Constitutes a Closed Path?
At its core, a **closed path**—often called a **closed curve** or **closed loop** in mathematics—is simply a path that starts and finishes at the same spot. Think of it as a journey where your ending point is also your beginning point. This seemingly small detail has big implications across different fields, providing a way to analyze things that repeat and systems that are interconnected.
In mathematical terms, a path can be described by a continuous function that maps a certain interval to a space. For this path to be considered closed, the function's value at the beginning of the interval must be exactly the same as its value at the end. This ensures a seamless connection, forming a complete circuit.
Consider a closed path not just as a shape, but as a representation of a series of states or events that returns to its original setup. This way of looking at it is super important in areas like computer science, where algorithms might follow closed paths, or in control systems, where feedback loops create closed paths for information to flow.
The beauty of the closed path is how self-contained it is. There are no loose ends; everything connects back to itself. This makes it incredibly valuable for modeling things where cycles are natural, from a planet's orbit to the repetitive actions inside a machine.

Geometric Phase In Composite Systems Ppt Download
The Significance of Closed Paths in Physics and Engineering
Energy Conservation and Circuitry
When we move into the world of physics, the concept of a closed path becomes even more important, especially when talking about conservative forces and keeping energy stable. For a **conservative force field**, the work done on an object moving along any closed path is always zero. This is a powerful rule, directly linked to the idea that energy isn't lost within these kinds of systems.
In electrical engineering, the idea of a closed path is absolutely essential. An electrical circuit, by its very nature, has to be a closed path for current to move. Electrons need a continuous loop to travel from the power source, through various components, and back to the source. Break that path anywhere, and—whoosh!—no current, no light, no power.
Think about a basic light bulb hooked up to a battery. The wires, the bulb's filament, and the battery itself all form a closed loop. If any part of this loop gets disconnected, the circuit is open, and the light stays stubbornly dark. Understanding this is crucial for designing everything from simple household appliances to complex electronic systems.
What's more, in how fluids move, ideas like **circulation around a closed path** are vital for understanding things like how an airplane wing creates lift. The mathematical tools developed for analyzing closed paths give engineers the means to predict and control how various physical systems behave, making sure things work efficiently and safely.

Focus On Open Paths Not Closed Wealth Affirmations, Book
Closed Paths in the World of Mathematics: Topology and Graph Theory
Loops and Cycles in Abstract Spaces
Mathematics offers a more abstract, yet incredibly insightful, way to look at closed paths. In **topology**, a branch of math that studies the properties of shapes that stay the same even when stretched or bent, closed paths are often called **loops**. These loops are key to understanding the "holes" or how connected a topological space is. Imagine a donut versus a sphere; the donut has a "hole" that allows for a distinct closed path around it, while any closed path on a sphere can be shrunk down to a single point.
Graph theory, another fascinating area of mathematics, deals with networks of points (called **vertices**) connected by lines (called **edges**). Here, a closed path is known as a **cycle**. Cycles are critical for understanding the structure and characteristics of networks, whether it's a social network, a computer network, or a road system. Knowing if cycles exist, or where they are, can tell us a lot about how efficient, redundant, and secure a system is.
Consider a transportation network. A closed path or cycle would be a route that brings you right back to your starting location. Figuring out these cycles is super important for making delivery routes better, understanding traffic flow, and even designing infrastructure that's more resilient. Without cycles, every journey would be a one-way trip, which sounds like quite the logistical nightmare, doesn't it?
Studying closed paths in these abstract mathematical frameworks gives us powerful tools to analyze real-world problems. It lets us look beyond just the physical meaning and explore the deeper structural qualities that govern various systems, leading to a more complete and general understanding.
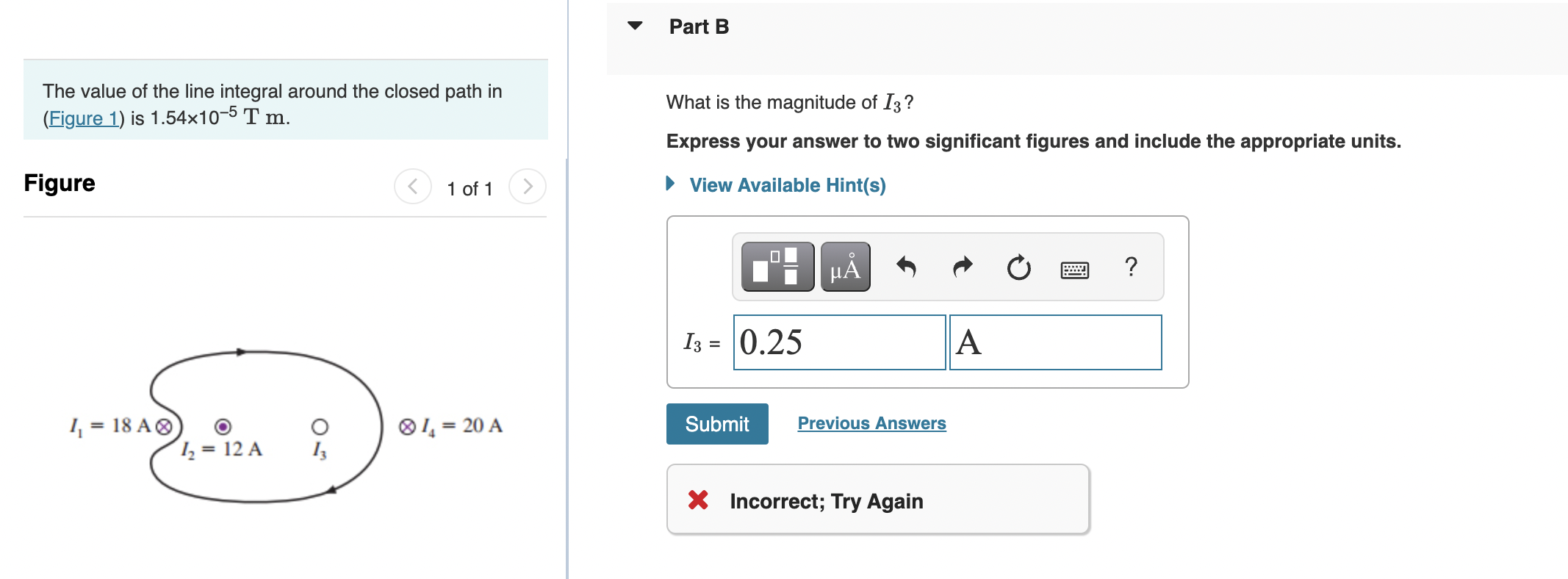
Solved The Value Of Line Integral Around Closed Path
Everyday Examples and the Ubiquity of Closed Paths
From Commutes to Coffee Machines
While the formal definitions might sound a bit like something from a textbook, closed paths are actually all around us, influencing our daily lives in ways we often don't even notice. Your morning commute, if you leave home and come back, is a perfect example of a closed path. Even just walking around the block and ending up where you started counts as a closed path.
Think about the **circulatory system** in your body. It's a fantastic example of a complex closed path, with blood constantly flowing from your heart, through your arteries, tiny capillaries, and veins, and then back to your heart. Without this incredibly intricate closed system, life as we know it simply wouldn't be possible. It's truly an amazing feat of biological design!
Even your coffee machine relies on a closed path to work. Water is pulled from a tank, heated up, sent through the coffee grounds, and then the brewed coffee comes out. While the water itself doesn't usually go directly back into the tank in a perfect loop, the overall system for making coffee can be seen as a series of connected closed paths for different things, like water and heat, to flow.
From the soft hum of a fan—where the blades move in a repeated, almost circular motion—to the grand orbits of planets around the sun, **closed paths** are a vital part of how the universe works and how we experience our everyday lives. Once you start looking, you'll see them everywhere, proving just how fundamental they are.
Frequently Asked Questions About Closed Paths
Your Burning Questions Answered!
Q1: Is a straight line considered a closed path?
A straight line, by itself, generally isn't thought of as a closed path unless the starting and ending points are exactly the same. Imagine drawing a line segment on paper. You begin at point A and end at point B. If A and B are different, it's an open path. However, if you "draw" just a single point, that could technically be seen as a really simple closed path where the start and end are the same and there's no actual movement. But in most real-world and theoretical situations, a closed path means there's some kind of journey or extent involved.
Q2: Can a closed path cross over itself?
Absolutely! A closed path can definitely intersect itself. Think about drawing the number "8" or an infinity symbol. Both are closed paths because they start and end at the same place, but they clearly cross over themselves. In mathematics, these are often called "self-intersecting loops" or "self-intersecting cycles," and their characteristics can be quite interesting to study in fields like knot theory.
Q3: What's the difference between a closed path and a cycle in graph theory?
In graph theory, a "cycle" is a very specific kind of closed path. While all cycles are closed paths, not every closed path is a cycle. A cycle in graph theory is a closed path that doesn't repeat any vertices (except for the one where it starts and ends) and doesn't repeat any edges. If a closed path repeats vertices or edges before getting back to the start, it would be a closed path but not a simple cycle. Think of it like this: a cycle is the "cleanest" type of closed path in a graph, without any unnecessary detours within the loop itself.